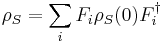Reduced dynamics
In quantum mechanics, especially in the study of open quantum systems, reduced dynamics refers to the time evolution of a density matrix for a system coupled to an environment. Consider a system and environment initially in the state 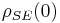 (which in general may be entangled) and undergoing unitary evolution given by
(which in general may be entangled) and undergoing unitary evolution given by 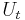 . Then the reduced dynamics of the system alone is simply
. Then the reduced dynamics of the system alone is simply
If we assume that the mapping 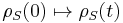 is linear and completely positive, then the reduced dynamics can be represented by a quantum operation. This mean we can express it in the operator-sum form
is linear and completely positive, then the reduced dynamics can be represented by a quantum operation. This mean we can express it in the operator-sum form
where the 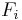 are operators on the Hilbert space of the system alone, and no reference is made to the environment. In particular, if the system and environment are initially in a product state
are operators on the Hilbert space of the system alone, and no reference is made to the environment. In particular, if the system and environment are initially in a product state 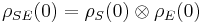 , it can be shown that the reduced dynamics are completely positive. However, the most general possible reduced dynamics are not completely positive.[1]
, it can be shown that the reduced dynamics are completely positive. However, the most general possible reduced dynamics are not completely positive.[1]
Notes
- ^ P. Pechukas, Reduced Dynamics Need Not Be Completely Positive. Physical Review Letters 73, 1060 (1994).
References
- Nielsen, Michael A. and Isaac L. Chuang (2000). Quantum Computation and Quantum Information, Cambridge University Press, ISBN 0-521-63503-9
![\rho_S (t) = \mathrm{Tr}_E [U_t \rho_{SE} (0) U_t^\dagger]](/2012-wikipedia_en_all_nopic_01_2012/I/7acb5bc2e39e491f4db0ba1b7f14a6bb.png)